Record Linking
Entity Resolution with Postgresql & Madlib
Created by Robert Berry / @no0p_
The world is full of messy data
Record linking solves one specific data quality problem.
Record Linking is ...
Two or more records,
referencing the same entity,
without a key.
Don't take my word for it
“Record linkage refers to the task of finding records in a data set that refer to the same entity across different data sources.
Record linkage is necessary when joining data sets based on entities that may or may not share a common identifier”

Some records in these tables refer to the same entity
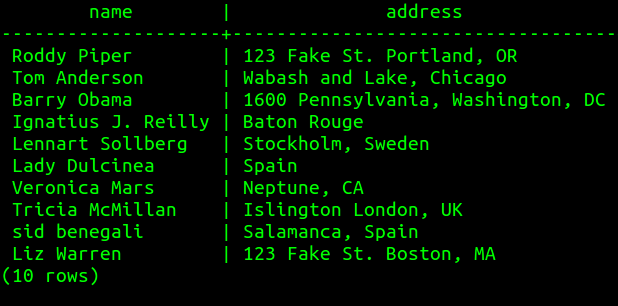 | 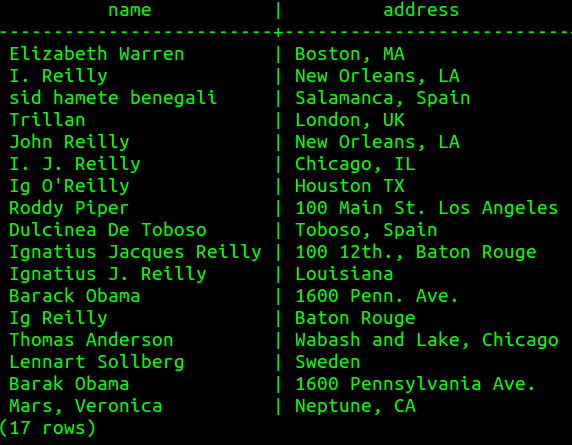 |
But how can we discern which are matches without a key?
Name & Conquer
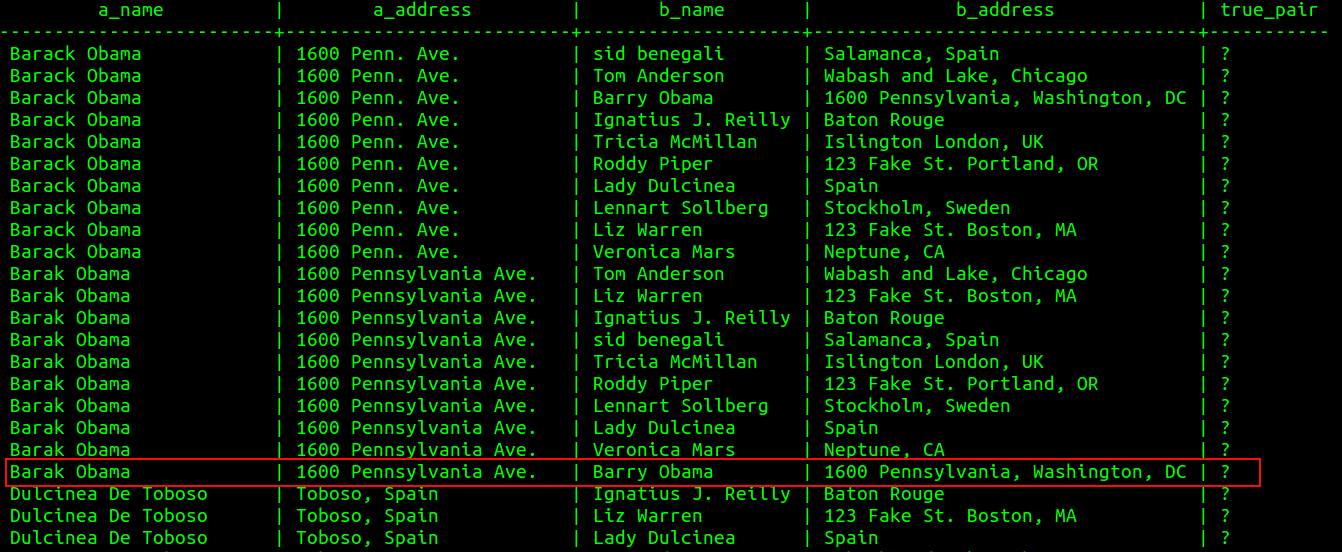
Label the records in table1 as set A, the records in table2 as set B.
Define a set of possible matches as A X B, such that each pair (a∈A,b∈B) is a possible match or non-match.
The set of true pairs is labeled set T where (a=b), and the set of false pairs is labeled set F where (a≠b).
Solve the problem by distinguishing whether a given pair belongs to set T or set F.
T and F are a partition of A X B.
In other words
each tuple in the cross join is either a true pair or a false pair
A Binary Classification Problem
Which is resolved by a function returning the probability that any old tuple from A and any old tuple from B are a true pair.
$P(truepair) = f(a, b)$
This is probably not the "function" you are looking for

Actually the function's parameters are properties of a tuple pair
$P(truepair) = f(a, b) = f(x_1, x_2, x_3, \ldots x_n)$
Where $x_1, x_2, \ldots x_n$ are numeric metrics of the pairing
Metrics Like Jaro-Winkler Distance
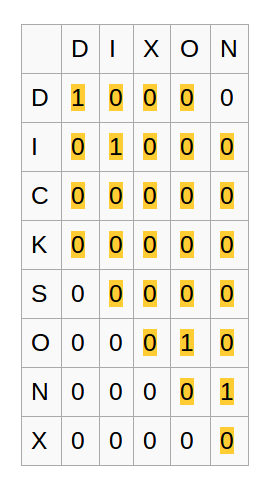
$d_j = \frac{1}{3}(\frac{m}{|s_1|} + \frac{m}{|s_2|} + \frac{m - t}{m})$
Where:
$m$ is the number of matching characters.
$t$ is half the number of transpositions.
Metrics Like...
| Levenshtein Distance of Name | $\mathbb{Z}$ |
| Trigram Distance of Name | $[0,1]$ |
| Geo Spatial Distance of Address | $\mathbb{R}$ |
| Name Shares Middle Initial Character | $0/1$ |
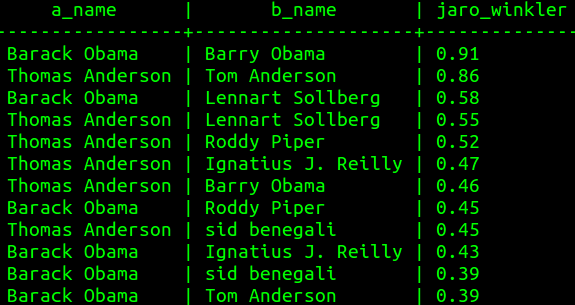
Jaro-Winkler Example
Trigram Example
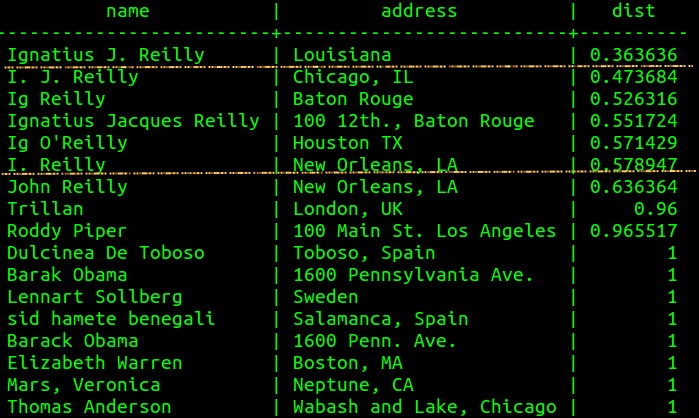
What is the optimal threshold?
Logistic Regression Provides the Function
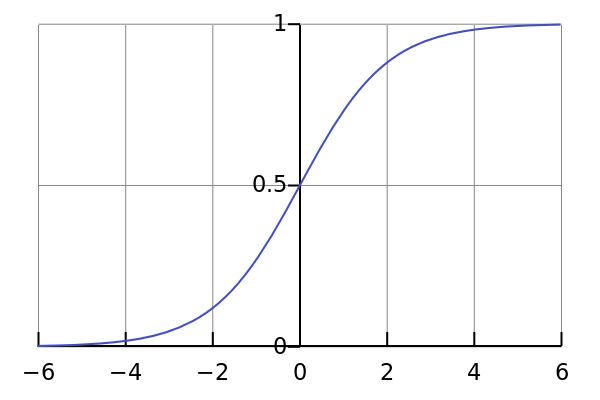
$P(true pair) = g(t) = \frac{1}{1 + e^{-t}}$
$t = \beta_0 + \beta_1x_1 + \ldots \beta_nx_n$
Logistic regression mathematically links features of tuple pairs to a probability the pair belongs to the set of true pairs T or the set of false pairs F
Barack Obama vs. Barry Obama
$x_1$ = Jaro Winkler Distance = 0.89
$x_2$ = Trigram Distance = 0.2
$P(true pair) = f(x_1, x_2) = \frac{1}{1 + e^{-(\beta_0 + \beta_1x_1 + \beta_2x_2)}}$
Logistic regression model solves for $\beta$ coefficients to complete equation.
One more note on features
Can derive features from joined tables
| Same Company/Organization/Relation | $0/1$ |
| Date/Time of Overlapping Activity | $\mathbb{R}$ |
| Geo Spatial Distance of Record or Relation | $\mathbb{R}$ |
| Same Phone Number | $0/1$ |
Implement this with Madlib
Madlib Provides Stuff Like
- Regression Models
- Tree Models
- Conditional Random Field
- ARIMA
- Latent Dirichlet Allocation
- K-means clustering
- Descriptive Statistics
- Inference
- SVM
- Cardinality Estimators
- Utility Functions and Types
Installation
pgxnclient install madlib
Configure; make
madpack -p postgres -c user@0.0.0.0/db install
Madlib's M.O.
Create training tables, apply SQL function, use model tables
Example Training Table
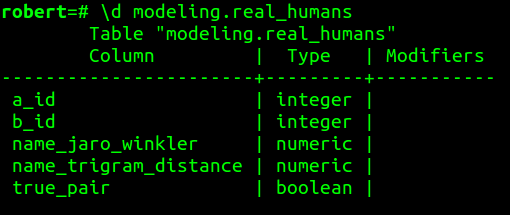
Populate Training Examples
Manually insert records into table.
Or leverage easily linkable records, e.g. 20% of company_a and company_b records have an IRS TID you can link on, but still have representative typo and alternative spelling examples.
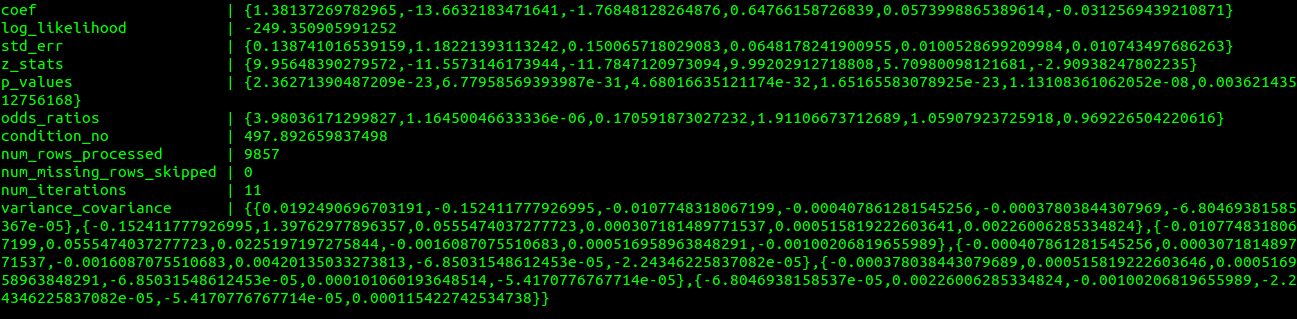
Training a Model
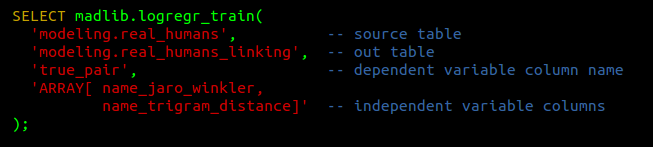
Provides coefficients for $t = \beta_0 + \beta_1x_1 + \ldots \beta_nx_n$
Making Predictions
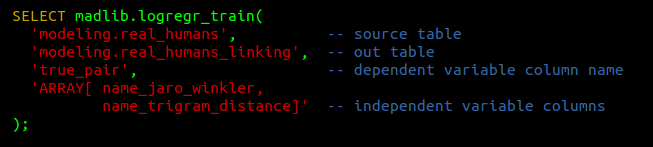
Returns a probability tuple pair is a true pair.
Evaluating the Model
$Accuracy = \frac{TP + TN}{TP + TN + FP + FN}$
$Precision = \frac{TP}{TP + FP}$
$Recall = \frac{TP}{TP + FN}$
Real World Results
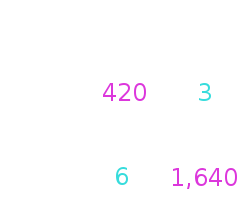
$Accuracy = \frac{TP + TN}{TP + TN + FP + FN} = 0.995$
$Precision = \frac{TP}{TP + FP} = 0.985$
$Recall = \frac{TP}{TP + FN} = 0.992$
Predictions
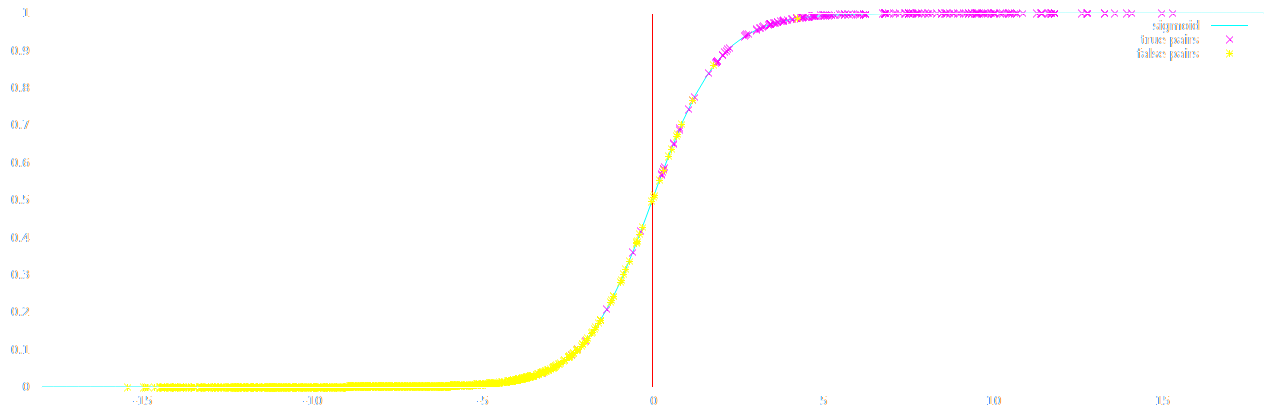
Distribution
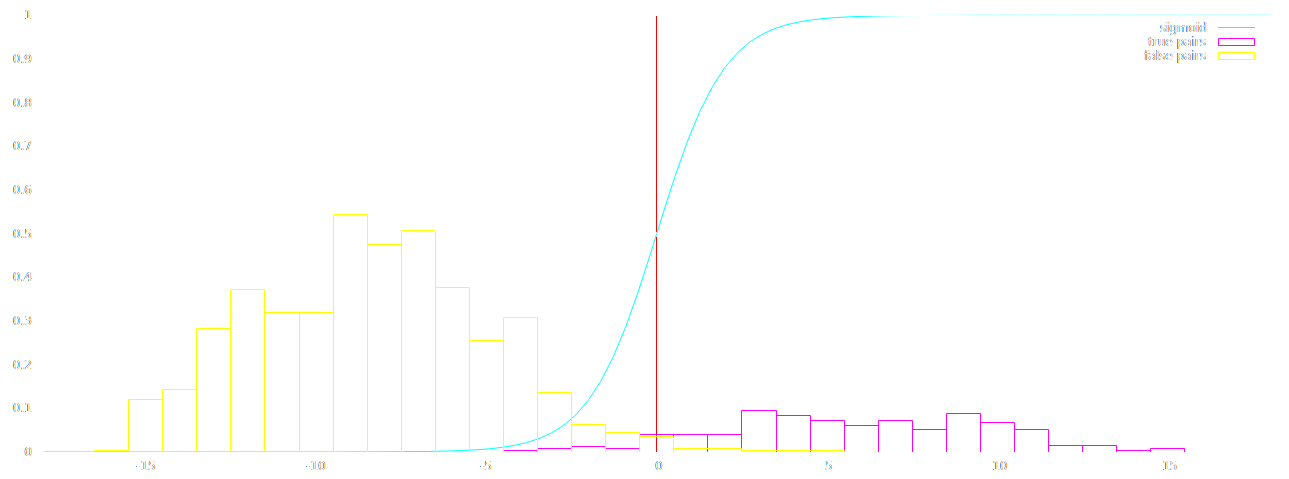
Less Successful Model
$Accuracy = \frac{TP + TN}{TP + TN + FP + FN} = 0.99$
$Precision = \frac{TP}{TP + FP} = 0.914$
$Recall = \frac{TP}{TP + FN} = 0.662$
Model only had name string as a parameter. Poor recall results.
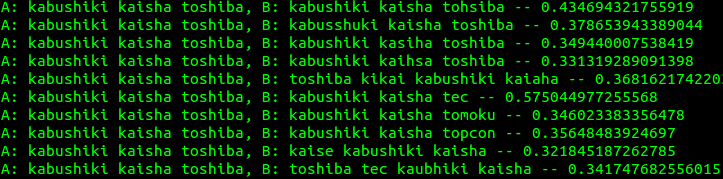
Scoring Examples

Scoring Examples
Model Information Table

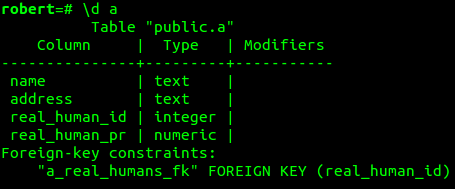
- Does not require application changes
- Preserves Original Information
- 'Probabilistic Foreign Key' Sounds fun
- Reasonably Painless Access Pattern
- Duplication and Linking Case
- Manual Review
What about that cross product?
- M*N ~ (N^2) pair comparisons to find best match
- Compare only against best candidates
- Indexable value that can exclude candidates
- trigram distance
- Geographic restriction
- Kmeans cluster id
- LSH bucket
- Probably OK to have fairly loose comparison set
Identify Problem as multiple records for same entity without a key
This can be formulated as a binary classification of paired records as members of a set of true pairs or false pairs in A X B
Solve binary classification in Postgresql with Madlib logistic regression module
String metric features & features from relations
Create probabilistic foreign keys
Manually review close calls
Final Thoughts
- We should strive for correct data with referential integrity
- Be comfortable in a world of imperfect databases